26 ноября 2011 Автор КакПросто! В школьном курсе геометрии ученики в основном считают площади правильных многоугольников. Между тем, для решения множества практических задач нередко приходится иметь дело с неправильными геометрическими фигурами.
- Как найти площадь полукруга Вопрос «Как определить объем трубы?Если ее длина 200м а диаметр 65мм.» — 4 ответа Вам понадобится
- — неправильная геометрическая фигура;-
- Как найти площадь поверхности
- Как рассчитать площадь неправильного многоугольника с разными сторонами
- Правильный многоугольник
- Узнать площадь многоугольника по периметру онлайн
- Калькулятор площади многоугольника
- Как узнать площадь многоугольника?
- Площадь многоугольника через радиус вписанной окружности
- Формула для расчета площади неправильного многоугольника
- Как найти площадь многоугольника
- Правильные многоугольники
- Формулы для стороны, периметра и площади правильного n – угольника
- Формулы для стороны, периметра и площади правильного треугольника
- Формулы для стороны, периметра и площади правильного шестиугольника
- Формулы для стороны, периметра и площади квадрата
- Как найти площадь многоугольника
- 1 Как найти площадь многоугольника – треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- 2 Как найти площадь многоугольника – квадрат
- 3 Как найти площадь многоугольника – прямоугольник
- 4 Как найти площадь многоугольника – трапеция
- 5 Площадь правильного многоугольника
- 6 Площадь неправильного многоугольника
- Периметр многоугольника
- Периметр прямоугольника
- Периметр треугольника
- Советуем посмотреть:
- Правило встречается в следующих упражнениях:
- Как найти площадь правильного и неправильного шестиугольника?
- Площадь правильного шестиугольника
- Площадь неправильного шестиугольника
- Площадь равностороннего шестиугольника
- 📺 Видео
Как рассчитать площадь неправильного многоугольника с разными сторонами
К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон.
Многие морские организмы обладают пентасимметрией, и наиболее очевидным примером невыпуклой фигуры является морская звезда. Правильные геометрические фигуры наоборот широко встречаются в природе.
Наиболее очевидным примером являются пчелиные соты, каждая ячейка которых представляет собой гексагон. Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
Правильный многоугольник
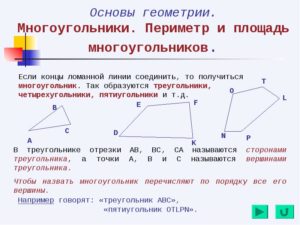
— плоская замкнутая ломаная, состоящая из прямых отрезков.
Расчет площади многоугольника по длине стороны:[ ((длина стороны)2×N)/(4Tan(π/N)) ] Введите длину стороны = Введите количество сторон = Площадь многоугольника = Расчет площади многоугольника используя радиус (описанной окружности):[ ½×R²×Sin(2π/N) ] Введите радиус = Введите кол-во сторон = Площадь Многоугольника = Расчет площади многоугольника, используя радиус вписанного круга: [ A²×N×Tan(π/N) ][ Apothem(A) = R×Cos(π/N) ] Введите радиус = Введите кол-во сторон = Площадь Многоугольника = Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет периметра Многоугольника:[ N×(side) ] Введите длину стороны = Введите кол-во сторон = Периметр Многоугольника = Расчет площади по длине стороны:
Узнать площадь многоугольника по периметру онлайн
Это может быть:
- пяти- или шестиугольник и так далее.
- треугольник;
- четырехугольник;
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне.
Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю.
Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет площади по длине стороны:Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности :Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга :Площадь Многоугольника = A² * N * Tan(π / N)где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны :Площадь Многоугольника = (A * P) / 2где A = сторона / (2 * Tan(π / N))где,
Калькулятор площади многоугольника
Фигура {$ main.figures $} Рассчитываем {$ main.types $} Радиус или диаметр Стороны или диагонали Введите 2 величины Сторона a Сторона b Диагонали Угол α {$ main.angles $} Угол β {$ main.angles $} Введите любые 3 величины Сторона A Сторона B Сторона C Угол α {$ main.
angles $} Угол β {$ main.angles $} Угол γ {$ main.angles $} Введите 2 величины Сторона A Сторона B Сторона C Угол α {$ main.angles $} Угол β {$ main.angles $} Введите 2 величины Сторона Высота Диагональ 1 Диагональ 2 Угол α {$ main.angles $} Угол β {$ main.angles $} Введите любые 3 величины Сторона A Сторона B Высота ha Высота hb Диагональ 1 Диагональ 2 Угол α {$ main.angles $} Угол β {$ main.angles
angle] $} Введите любые 3 величины Основание A Основание C Высота H Дополните боковые стороны для поиска периметра Сторона B Сторона D Введите 1 величину Сторона A Радиус описанной окружности (R) Радиус вписанной окружности (r) Количество сторон многоугольника Введите 1 величину Сторона A Радиус описанной окружности (R) Радиус вписанной окружности (r) Введите 1 величину Сторона A = радиусу описанной окружности (R) Радиус вписанной окружности (r) Рассчитать Результат расчета
[/attention]
- Периметр: {$ result.p|number:4 $}
- Площать: {$ result.s|number:4 $}
Многоугольник или полигон — геометрическая фигура, которая имеет n-ное количество углов.
Как узнать площадь многоугольника?
January 6, 2016 Обсудить 0 0 В задачах по геометрии часто требуется вычислить площадь многоугольника.
https://www.youtube.com/watch?v=BebF9D4F410
Причем он может иметь довольно разнообразную форму – от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми.
В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры.
Они дают название получившейся фигуре. Это может быть:
- четырехугольник;
- треугольник;
- пяти- или шестиугольник и так далее.
Такая фигура
Площадь многоугольника через радиус вписанной окружности
В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность.
Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.
Нарисуем многоугольник A1A2A3A4A5, не обязательно правильный, но такой, в который можно вписать окружность.
Напомню, что вписанной называется окружность, которая касается всех сторон многоугольника.
На рисунке это зелёная окружность с центром в точке O: Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».
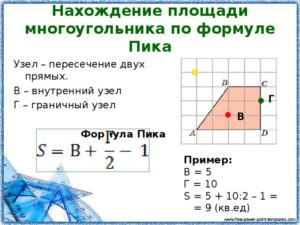
Формула для расчета площади неправильного многоугольника
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2020 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Как найти площадь многоугольника
Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник.
Видео:Сможете ли вы посчитать периметр каждой из этих двух фигур?Скачать

Правильные многоугольники
| О нас |
| Демоверсии |
| Учебные пособия |
| Справочник по математике |
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.
Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.
Замечание 1. В любой правильный многоугольник можно вписать окружность.
Замечание 2. Около любого правильного многоугольника можно описать окружность.
Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Используемые обозначения
| Число вершин правильного многоугольника | Сторона правильного многоугольника | Радиус вписанной окружности | Радиус описанной окружности | Периметр | Площадь |
| n | a | r | R | P | S |
| Число вершин правильного многоугольника | n |
| Сторона правильного многоугольника | a |
| Радиус вписанной окружности | r |
| Радиус описанной окружности | R |
| Периметр | P |
| Площадь | S |
Формулы для стороны, периметра и площади правильного n – угольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = an | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Площадь | Выражение площади через сторону | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного n – угольника |
| Выражение периметра через сторонуP = anВыражение периметра через радиус вписанной окружностиВыражение периметра через радиус описанной окружности |
| Формулы для площади правильного n – угольника |
| Выражение площади через сторону и радиус вписанной окружностиВыражение площади через сторонуВыражение площади через радиус вписанной окружностиВыражение площади через радиус описанной окружности |
| Формулы для стороны правильного n – угольника |
| Выражение стороны через радиус вписанной окружностиВыражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного треугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 3a | Выражение периметра через сторону | |
| Площадь | Посмотреть вывод формулы | Выражение площади через сторону | |
| Площадь | Выражение площади через сторону и радиус вписанной окружности | ||
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | Посмотреть вывод формулы | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного треугольника |
| Выражение периметра через сторонуP = 3aВыражение периметра через радиус вписанной окружностиВыражение периметра через радиус описанной окружности |
| Формулы для площади правильного треугольника |
| Выражение площади через сторонуПосмотреть вывод формулыВыражение площади через сторону и радиус вписанной окружностиВыражение площади через радиус вписанной окружностиПосмотреть вывод формулыВыражение площади через радиус описанной окружностиПосмотреть вывод формулы |
| Формулы для стороны правильного треугольника |
| Выражение стороны через радиус вписанной окружностиВыражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного шестиугольника
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 6a | Выражение периметра через сторону | |
| Площадь | Выражение площади через сторону | ||
| Площадь | S = 3ar | Выражение площади через сторону и радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус вписанной окружности | ||
| Периметр | Выражение периметра через радиус вписанной окружности | ||
| Площадь | Выражение площади через радиус вписанной окружности | ||
| Сторона | a = R | Выражение стороны через радиус описанной окружности | |
| Периметр | P = 6R | Выражение периметра через радиус описанной окружности | |
| Площадь | Выражение площади через радиус описанной окружности |
| Формулы для периметра правильного шестиугольника |
| Выражение периметра через сторонуP = 6aВыражение периметра через радиус вписанной окружностиВыражение периметра через радиус описанной окружностиP = 6R |
| Формулы для площади правильного шестиугольника |
| Выражение площади через сторонВыражение площади через сторону и радиус вписанной окружностиS = 3arВыражение площади через радиус вписанной окружностиВыражение площади через радиус описанной окружности |
| Формулы для стороны правильного шестиугольника |
| Выражение стороны через радиус вписанной окружностиВыражение стороны через радиус описанной окружностиa = R |
Формулы для стороны, периметра и площади квадрата
| Величина | Рисунок | Формула | Описание |
| Периметр | P = 4a | Выражение периметра через сторону | |
| Площадь | S = a2 | Выражение площади через сторону | |
| Сторона | a = 2r | Выражение стороны через радиус вписанной окружности | |
| Периметр | P = 8r | Выражение периметра через радиус вписанной окружности | |
| Площадь | S = 4r2 | Выражение площади через радиус вписанной окружности | |
| Сторона | Выражение стороны через радиус описанной окружности | ||
| Периметр | Выражение периметра через радиус описанной окружности | ||
| Площадь | S = 2R2 | Выражение площади через радиус описанной окружности |
| Формулы для периметра квадрата |
| Выражение периметра через сторонуP = 4aВыражение периметра через радиус вписанной окружностиP = 8rВыражение периметра через радиус описанной окружности |
| Формулы для площади квадрата |
| Выражение площади через сторонуS = a2Выражение площади через радиус вписанной окружностиS = 4r2Выражение площади через радиус описанной окружностиS = 2R2 |
| Формулы для стороны квадрата |
| Выражение стороны через радиус вписанной окружностиa = 2rВыражение стороны через радиус описанной окружности |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Видео:Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Как найти площадь многоугольника
Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.
1
Как найти площадь многоугольника – треугольник
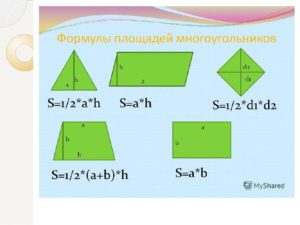
- S = 1/2×h×b, где h – высота, а b – сторона.
- S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
- S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
- S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
- S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.
Прямоугольный треугольник
- S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
- S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
- S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.
Равнобедренный треугольник
- S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
- S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.
Равносторонний треугольник
- S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
- S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
- S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
- S = h²/√3, где h – высота равностороннего треугольника.
2
Как найти площадь многоугольника – квадрат
- S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
- S = d²/2, где d – диагональ квадрата.
3
Как найти площадь многоугольника – прямоугольник
- S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
- S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5². x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²
4
Как найти площадь многоугольника – трапеция
- S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
- S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
- S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
- S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.
S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.
5
Площадь правильного многоугольника
- S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
- S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.
6
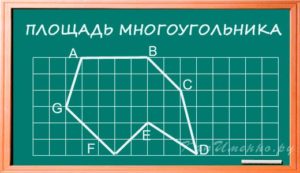
Площадь неправильного многоугольника
Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:
- Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
- Умножаем значение x одной вершины на значение y второй и так далее.
- Складываем все значение, получаем какое-то число.
- Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.
- От суммы значений первой таблицы отнимаем сумму значений второй таблицы.
- Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.
Первая полоса
Беременность
Как не набрать лишний вес во время беременности
Видео:Самый простой способ нахождения площадиСкачать

Периметр многоугольника
Любой многоугольник — это замкнутая ломаная линия.
Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.
Значит, периметр многоугольника — это сумма длин всех его сторон.
В математике периметр обозначают буквой P (пэ).
Периметр прямоугольника
Например, найдём периметр данного прямоугольника.
1 способ:
Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.
2 способ:
Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.
Формула для подсчета периметра прямоугольника:
(a + b) • 2
a – длина прямоугольника
b – ширина прямоугольника.
https://www.youtube.com/watch?v=jCtM27FFZ9I
Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:
Периметр треугольника
Периметр квадрата
Первый способ (когда мы еще не знаем действие умножения):
Второй способ (когда мы изучили действие умножения):
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Площадь фигуры
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 67, Моро, Волкова, Рабочая тетрадь, 1 часть
Задание 131, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 17, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 50, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 67, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 78, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 76, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 8, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 75, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 15. Вариант 2. № 2, Моро, Волкова, Проверочные работы
Страница 33. Вариант 2. № 2, Моро, Волкова, Проверочные работы
4 класс
Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 43, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 48, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 51, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 71, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 14, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Задание 207, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 208, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 210, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
6 класс
Задание 389, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 428, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 430, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Нашли ошибку?
Связаться с нами
Видео:Как посчитать площадь многоугольника за 15 секунд в уме? Формула для ленивыхСкачать

Как найти площадь правильного и неправильного шестиугольника?
Умение определять площадь различных фигур играет немалуюроль в жизни каждого человека. Рано или поздно приходится иметь дело с этимизнаниями. К примеру, в процессе ремонта помещения для определения необходимогоколичества рулонов обоев, линолеума, паркета, плитки в ванную или на кухнюнужно уметь рассчитывать необходимую площадь.
Знаниями в области геометрии пользовались еще в древнемВавилоне и других странах. На первых шагах к культуре всегда возникаланеобходимость измерить участок, расстояние. При строительстве первыхзначительных сооружений требовались умения выдерживать вертикаль,спроектировать план.
Роль эстетических потребностей людей также имела немалоезначение. Украшение жилища, одежды, рисование картин способствовало процессуформирования и накопления сведений в области геометрии, которые люди тех времёндобывали опытным путем, по крупицам и передавали из поколения в поколение.
https://www.youtube.com/watch?v=aayJKa6lGaw
Сегодня знания геометрии необходимы и закройщику, и строителю,и архитектору и каждому простому человеку в быту.
Поэтому нужно учиться рассчитывать площадь различныхфигур, и помнить, что каждая из формул может пригодиться впоследствии напрактике, в том числе, и формула правильного шестиугольника. Шестиугольником называетсятакая многоугольная фигура, общее количество углов которой равно шести.
Площадь правильного шестиугольника
Правильным шестиугольником называют шестиугольную фигуру,которая имеет равные стороны. Углы у правильного шестиугольника также междусобой равны.
В повседневной жизни мы часто можем встретить предметы,имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейкипчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняютсяплоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, какплитка укладывается одна возле другой, не оставляя пустых мест.
Свойстваправильного шестиугольника
- Правильный шестиугольник всегда будет иметь равные углы,каждый из которых составляет 120˚.
- Сторона фигуры равняется радиусу описанной окружности.
- Все стороны в правильном шестиугольнике равны.
- Правильный шестиугольник плотно заполняет плоскость.
Как посчитатьплощадь правильного шестиугольника?
Площадь правильного шестиугольника можно рассчитать,разбив его на шесть треугольников, каждый из которых будет иметь равныестороны.
Для расчета площади правильного треугольника используетсяследующая формула:Зная площадь одного из треугольников, можно легкорассчитать площадь шестиугольника. Формула для ее расчета проста: посколькуправильный шестиугольник — это шесть равных треугольников, следует площадьнашего треугольника умножить на 6.
Если провести от центра фигуры к любой из ее сторонперпендикуляр, получим отрезок, который называется апофема. Рассмотрим, какнайти площадь шестиугольника при известной апофеме:
- Площадь = 1/2*периметр*апофему.
- Предположим, наша апофема равняется 5√3 см.
- Используя апофему, находим периметр: Поскольку апофемарасположена перпендикулярно к стороне шестиугольника, то углы треугольника,созданного при помощи апофемы, будут равняться 30˚—60˚—90˚.
Каждая сторонаполученного треугольника будет соответствовать: x-x√3-2x,где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона,расположенная напротив угла в 60˚ — это x√3,а гипотенуза — 2x.
- Поскольку апофема представлена, как x√3, можно подставить ее в формулу a = x√3 и решить.
Если, к примеру,апофема = 5√3, тогда подставим этувеличину в формулу и получим: 5√3 см = x√3, или x = 5см.
- Итак, короткая сторона треугольника равняется 5 см.поскольку эта величина является половиной длины стороны шестиугольника,умножаем 5 на 2 и получим 10 см, которая является длиной стороны.
- Зная длину стороны, умножим её на 6 и получим периметршестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу:
Площадь =1/2*периметр*апофему
Площадь = ½*60см*5√3
Решаем:
Теперь осталось упроститьответ, чтобы избавиться от квадратных корней, а полученный результат укажем вквадратных сантиметрах:
½ * 60 см * 5√3 см =30 * 5√3см =150 √3 см =259.8 см²
о том, как найти площадь правильного шестиугольника
Площадь неправильного шестиугольника
Существует несколько вариантов определения площадинеправильного шестиугольника:
- Метод трапеции.
- Метод расчета площади неправильных многоугольников припомощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будутизвестны, подбирается подходящий метод.
Метод трапеции
Площадь шестиугольника, имеющего произвольную(неправильную) форму, рассчитывается методом трапеции, суть которого состоит вразделении шестиугольника на отдельные трапеции и последующим вычислениемплощади каждой из них.
Метод с осямикоординат
Кроме этого, площадь неправильного шестиугольника можно рассчитатьпри помощи метода расчета площади неправильных многоугольников. Рассмотрим егона следующем примере:
Вычисление будем выполнять методом использованиякоординат вершин многоугольника:
- На этом этапе следует сделать таблицу и записатькоординаты вершин x и y. Выбираем вершины впоследовательном порядке по направлению против часовой стрелки, завершив конецсписка повторной записью координаты первой вершины:
- Теперь следует умножить значения координаты х 1-й вершинына y 2-йвершины и продолжить таким образом умножение далее. Затем необходимо сложитьполученные результаты. В нашем случае получилось 82:
- Последовательно умножаем значения координат y1-йвершины на значения координат х 2-й вершины. Суммируем полученные результаты. Внашем случае получилось 38:
- Вычитаем сумму, которую получили на четвертом этапе изсуммы, которая получилась на третьем этапе: 82 – (-38) = 120
- Теперь необходимо разделить результат, который былполучен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60см²
Метод разбиванияшестиугольника на другие фигуры
Каждый многоугольник можно разделить на несколько другихфигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя изизвестных данных, пользуясь формулами определения площадей перечисленных фигур,последовательно вычисляются их площади и затем суммируются.
https://www.youtube.com/watch?v=doTn3QzC8ds
Некоторые неправильные шестиугольники состоят из двухпараллелограммов. Для определения площади параллелограмма следует умножить егодлину на ширину и затем сложить две уже известные площади.
о том, как найти площадь многоугольника
Площадь равностороннего шестиугольника
Равносторонний шестиугольник имеет шесть равных сторон иявляется правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны,поэтому для нахождения площади такого шестиугольника достаточно будет знатьплощадь хотя бы одного треугольника.
Для нахождения площади равностороннего шестиугольникаиспользуется, конечно же, формула площади правильного шестиугольника, описаннаявыше.
📺 Видео
Площадь фигурыСкачать

ПЛОЩАДЬ МНОГОУГОЛЬНИКА 8 класс геометрия АтанасянСкачать

Что такое периметр. Как найти периметр многоугольника?Скачать

Как найти площадь фигуры?Скачать

Быстрый способ ➜ Найдите площадь многоугольника на рисункеСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задание №4 "найти площадь фигуры" по теме "Единицы измерения площади". Математика 4, 5 классСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Как различать периметр и площадь?Скачать

Видео урок гиа по математике 2013: Найти площадь фигуры.Скачать
Нахождение периметра и площади.Скачать

Площадь многоугольникаСкачать

Периметр многоугольникаСкачать